Thanks for the effort!
You’re welcome.
Thanks for the effort!
You’re welcome.
Just proves, never too late to learn :-)
I would have got 1 by doing 2(2+2) = 8 first. Not because of bracket but because of “implied multiplication.”
Yeah, right answer but wrong reason. There’s no such thing as implicit multiplication.
What I am learning here: 8÷2(2+2) is not same as 8÷2×(2+2)
Correct, and that’s because of Terms - 8÷2(2+2) is 2 terms, with the (2+2) in the denominator, but 8÷2×(2+2) is 3 terms, with the (2+2) in the numerator… hence why people get the wrong answer when they add an extra multiply in.
number next bracket is not the same as normal multiplication in rule book
Right, because it’s not “multiplication” at all (only applies literally to multiplication signs), it’s a coefficient of a bracketed term, which means we have to apply The Distributive Law as part of solving Brackets.
÷ & × have right of way rule with whoever is left most wins
Yeah, the actual rule is Left associativity, and going left to right is the easy way to obey that.
you’re just a tutor and not actually a teacher?
Both - see the problem with the logic you use?
Let me know when you decide to consult a textbook about this.
a single sentence of a wikipedia article without me handfeeding it to you
And I told you why it was wrong, which is why I read Maths textbooks and not wikipedia.
I’m sorry for your students
My students are doing good thanks

The notation is not intrinsically clear
It is to me, I actually teach how to write it.
Exactly! It’s in math textbooks, in both ways!
And both ways are explained, so not ambiguous which is which.
Ummm, I was agreeing with you??
Anyways, I’m a Maths teacher who has taught this topic many times - what would I know?
multiple always happens first. But apparently it’s what’s left side first
Multiplication and division are equal precedence (and done left to right) if that’s what you’re talking about, but the issue is that a(b+c) isn’t “multiplication” at all, it’s a bracketed term with a coefficient which is therefore subject to The Distributive Law, and is solved as part of solving Brackets, which is always first. Multiplication refers literally to multiplication signs, of which there are none in the original question. A Term is a product, which is the result of a multiplication, not something which is to be multiplied.
If a=2 and b=3, then…
axb=2x3 - 2 terms
ab=6 - 1 term
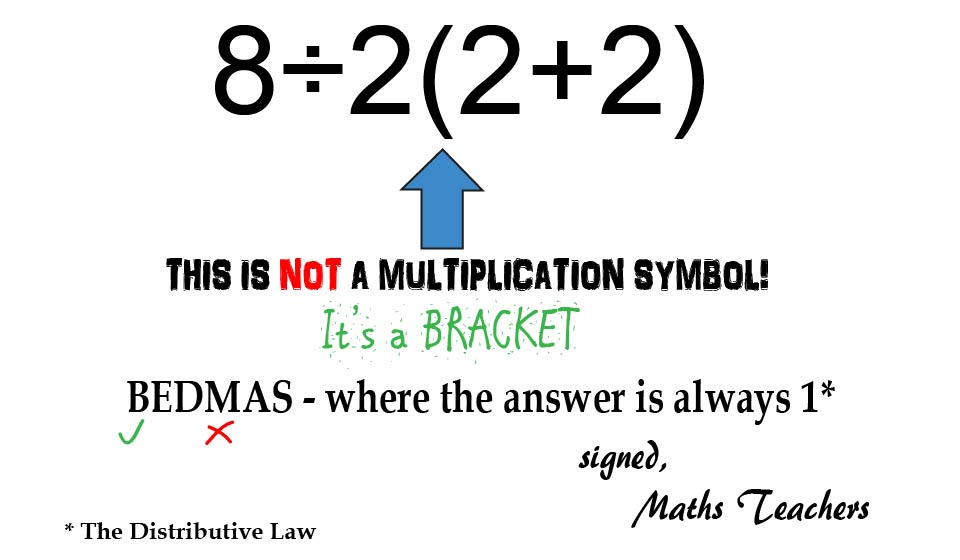
You can define your notation that way if you like
Nothing to do with me - it’s in Maths textbooks.
without knowing the conventions the author uses, it’s ambiguous
Well they should all be following the rules of Maths, without needing to have that stated.
which clearly states that the distributive property is a generalization of the distributive law
Let me say again, people calling a Koala a Koala bear doesn’t mean it actually is a bear. Stop reading wikipedia and pick up a Maths textbook.
You seem to be under the impression that the distributive law and distributive property are completely different statements
It’s not an impression, it’s in Year 7 Maths textbooks.
this certainly is not 7th year material
And yet it appears in every Year 7 textbook I’ve ever seen.
Looks like we’re done here.
If you read the wikipedia article
…which isn’t a Maths textbook!
also stating the distributive law, literally in the first sentence
Except what it states is the Distributive property, not The Distributive Law. If I call a Koala a Koala Bear, that doesn’t mean it’s a bear - it just means I used the wrong name. And again, not a Maths textbook - whoever wrote that demonstrably doesn’t know the difference between the property and the law.
This is something you learn in elementary school
No it isn’t. This is a year 7 topic. In Primary School they are only given bracketed terms without a coefficient (thus don’t need to know The Distributive Law).
be assured that I am sufficiently qualified
No, I’m not assured of that when you’re quoting wikipedia instead of Maths textbooks, and don’t know the difference between The Distributive Property and The Distributive Law, nor know which grade this is taught to.
Wikipedia is not intrinsically less accurate than maths textbooks
BWAHAHAHAHA! You know how many wrong things I’ve seen in there? And I’m not even talking about Maths! Ever heard of edit wars? Whatever ends up on the page is whatever the admin believes. Wikipedia is “like an encyclopedia” in the same way that Madonna is like a virgin.
but you are misunderstanding them
And yet you have failed to point out how/why/where. In all of your comments here, you haven’t even addressed The Distributive Law at all.
Whether you write it as a(b+c) = ab + ac or as a*(b+c) = ab + ac is insubstantial
And neither of those examples is about The Distributive Law - they are both to do with The Distributive Property (and you wrote the first one wrong anyway - it’s a(b+c)=(ab+ac). Premature removal of brackets is how many people end up with the wrong answer).
If I write f^{-1}(x), without context, you have literally no way of knowing whether I am talking about a multiplicative or a functional inverse, which means that it is ambiguous
The inverse of the function is f(x)^-1. i.e. the negative exponent applies to the whole function, not just the x (since f(x) is a single term).
Ok, that’s a start. In your simple example they are all equal, but they aren’t all the same.
yn+y - 2 terms
y(n+1) - 1 term
y×(n +1) - 2 terms
To see the difference, now precede it with a division, like in the original question…
1÷yn+y=(1/yn)+y
1÷y(n+1)=1/(yn+y)
1÷y×(n +1)=(n +1)/y
Note that in the last one, compared to the second one, the (n+1) is now in the numerator instead of in the denominator. Welcome to why having the (2+2) in the numerator gives the wrong answer.
Do you not understand that syntax is its own set of rules?
Yes, the rules of Maths, as I was already saying. I’m a Maths teacher. I take it you didn’t read the link then.
Please learn some math
I’m a Maths teacher - how about you?
Quoting yourself as a source
I wasn’t. I quoted Maths textbooks, and if you read further you’ll find I also quoted historical Maths documents, as well as showed some proofs.
I didn’t say the distributive property, I said The Distributive Law. The Distributive Law isn’t ax(b+c)=ab+ac (2 terms), it’s a(b+c)=(ab+ac) (1 term), but inaccuracies are to be expected, given that’s a wikipedia article and not a Maths textbook.
I did read the answers, try doing that yourself
I see people explaining how it’s not ambiguous. Other people continuing to insist it is ambiguous doesn’t mean it is.
The y(n+1) is same as yn + y
No, it’s the same as (yn+y). You can’t remove brackets unless there is only 1 term left inside.
if you removed the “6÷” part. It’s
…The Distributive Law.
That just states that a*(b + c) = ab + ac
No, The Distributive Law states that a(b+c)=(ab+ac), and that you must expand before you simplify.
For some simple exanples,
Examples by people who simply don’t remember all the rules of Maths. Did you read the answers?
If they weren’t ambiguous, then you wouldn’t see them getting popular
#MathsIsNeverAmbiguous They get popular because people who don’t remember all the rules of Maths want to argue with the people who do remember all the rules of Maths. #DontForgetDistribution
As a Maths teacher, almost daily 😂